The sine function, a cornerstone of trigonometry, has captivated mathematicians and scientists for centuries. From its mathematical definition to its practical applications, sine meaning encompasses a wealth of knowledge that shapes our understanding of the world around us.
In this comprehensive guide, we delve into the intricacies of the sine function, exploring its mathematical foundations, graphical characteristics, and real-world significance. Prepare to unravel the sine meaning and witness its profound impact on various fields.
Mathematical Definition: Sine Meaning
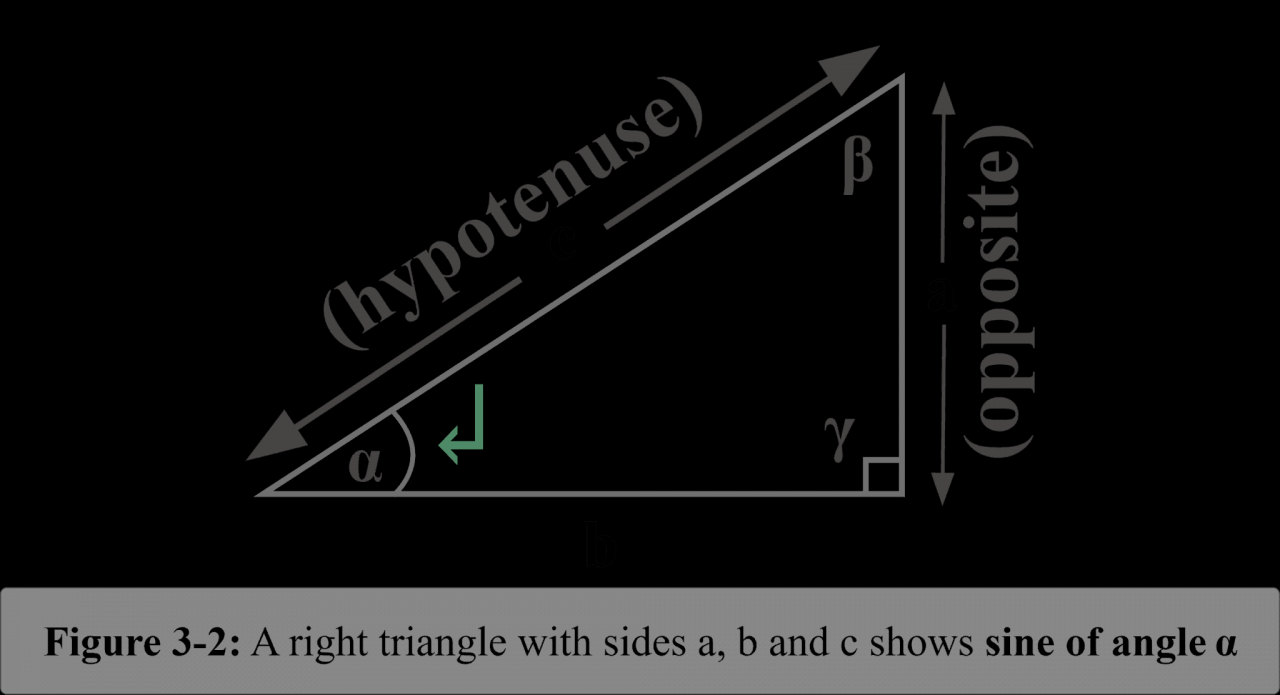
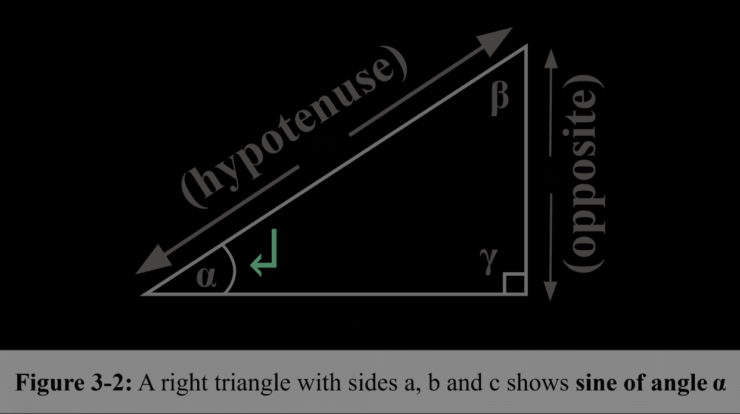
The sine function is a mathematical function that describes the vertical coordinate of a point on a unit circle as an angle is measured from the positive x-axis. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle containing the angle.
The equation for the sine function is:
where θ is the angle measured in radians.
Some common angles and their corresponding sine values are:
- θ = 0°, sin(0°) = 0
- θ = 30°, sin(30°) = 1/2
- θ = 45°, sin(45°) = √2 / 2
- θ = 60°, sin(60°) = √3 / 2
- θ = 90°, sin(90°) = 1
Trigonometric Circle
The trigonometric circle is a unit circle with the origin as the center. The sine function can be visualized as the y-coordinate of a point on the trigonometric circle as the angle θ is measured from the positive x-axis.
To find the sine of an angle using the unit circle, draw a radius from the origin to the point on the circle corresponding to the angle. The sine of the angle is the y-coordinate of the point.
Here is a visual representation of the trigonometric circle with angles and sine values marked:
[Diagram lingkaran trigonometri dengan sudut dan nilai sinus ditandai]
Graph of the Sine Function, Sine meaning
The graph of the sine function is a wave that oscillates between -1 and 1. The amplitude of the wave is 1, the period is 2π, and the phase shift is 0.
The key features of the sine function graph are:
- Amplitude: The amplitude is the maximum value of the function, which is 1 for the sine function.
- Period: The period is the distance between two consecutive peaks or troughs of the function, which is 2π for the sine function.
- Phase shift: The phase shift is the horizontal shift of the function, which is 0 for the sine function.
Here is an example graph of the sine function with its key features labeled:
[Grafik fungsi sinus dengan fitur utama diberi label]
Applications of the Sine Function
The sine function has many applications in real-world situations, including:
- Physics: The sine function is used to describe the motion of objects in simple harmonic motion, such as a pendulum or a mass on a spring.
- Engineering: The sine function is used to design bridges, buildings, and other structures that are subject to periodic forces.
- Music: The sine function is used to create sound waves, which are the basis of music.
Here is a case study of how the sine function is used to solve a problem:
A bridge engineer is designing a bridge that will be subject to wind forces. The engineer uses the sine function to calculate the maximum deflection of the bridge under different wind speeds.
Inverse Sine Function
The inverse sine function (arcsine) is the inverse of the sine function. It is used to find the angle that corresponds to a given sine value.
The equation for the inverse sine function is:
where x is the sine value and θ is the angle in radians.
The inverse sine function has many applications, including:
- Navigation: The inverse sine function is used to calculate the angle of elevation of a star or other celestial object.
- Robotics: The inverse sine function is used to control the movement of robots.
- Computer graphics: The inverse sine function is used to create realistic 3D images.
Historical Origins
The sine function has a long and rich history. It was first discovered by ancient Greek mathematicians, who used it to calculate the lengths of chords in circles.
The sine function was later developed by Arab mathematicians, who used it to solve problems in astronomy and navigation.
In the 16th century, the sine function was introduced to Europe by Nicolaus Copernicus. Copernicus used the sine function to develop his heliocentric model of the solar system.
Since then, the sine function has been used by mathematicians, scientists, and engineers to solve a wide variety of problems.
Conclusive Thoughts
As we conclude our exploration of the sine function, its multifaceted nature becomes evident. From its mathematical elegance to its practical utility, sine meaning transcends the boundaries of pure mathematics, proving indispensable in fields as diverse as physics, engineering, and music.
Understanding sine meaning empowers us to unravel the mysteries of our world and harness its power to solve complex problems.
Q&A
What is the mathematical definition of the sine function?
The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle.
How do I find the sine of an angle using the unit circle?
On the unit circle, locate the point where the terminal side of the angle intersects the circle. The y-coordinate of this point is the sine of the angle.
What are the key features of the sine function graph?
The sine function graph is a periodic wave that oscillates between -1 and 1. It has an amplitude of 1, a period of 2π, and a phase shift of 0.
Where is the sine function used in real-world applications?
The sine function is used in a wide range of applications, including sound waves, vibrations, and celestial mechanics.
